| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- conjunction
- negation
- functional symbol
- 논리학
- formal proof
- individual constants
- predicate symbols
- identity introduction
- fol
- disjunction
- 원자 명제
- atomic sentence
- truth table
- substitution
- terms
- transitivity of identity
- Validity
- Connectives
- first order logic
- reiteration
- soundness
- 개별 상수
- 1차 논리
- arguments
- identity elimination
- Today
- Total
컴공생의 공부LOG
[논리학] 2. The Logic of Atomic Sentences 본문
Arguments (논의, 논쟁)
- 한 개 이상의 전제(premises)와 결론(conclusion)이 모인 일련의 문장 모음
※ Functional symbols과 predicate의 인자로 들어가는 인자(argument)와 다른 의미라는 점 주의
ex) All men are mortal. Socrates is a man. So, Socrates is mortal.
전제1 : All men are mortal.
전제2 : Socrates is a man.
결론 : Socrates is mortal.
Logically Valid Arguments
- Argument 가 주어졌을 때, 아래의 경우 논리적으로 합당(logically valid)한 arguments 라고 함
=> 전제가 참일 때, 결론이 참인 경우
Logical Consequence
: Logically valid한 argument의 결론은 전제에 대하여 logical consequence라고 함
-> 즉, Logically valid -> Logical Consequence
※ 전제와 결론 구분 요령
-전제에 사용 : Because, since, after all
-결론 앞에 사용 : Hence, thus, so, consequently
Validity
Argument 1 : All men are mortal. Socrates is a man. So, Socrates is mortal.
Argument 2 : Lucretius is a man. After all, Lucretius is mortal and all men are mortal.
Argument 1번은 logically valid 또는 결론이 전제에 대하여 logical consequence.
-> why? 전제가 참일 때, 결론이 거짓일 수가 없음.
Argument 2번은 거짓이 될 수 있음. 전제가 참이더라도 결론이 거짓이 될 수 있음.
예를 들어, Lucretius가 금붕어 이름이라면 결론이 거짓이 됨.
Soundness
- 어떤 argument 가 valid 하고, 전제가 모두 참일 때, 이 argument를 sound 하다고 함.
Sound 예시
Argument : All men are mortal. Socrates is a man. So, Socrates is mortal.
-> valid한 argument이면서, sound 함
Sound 하지 않은 예시
Argument : All rich actors are good actors. Brad Pitt is a rich actor. So, he must be a good actor.
-> valid 하지만 sound 하지 않음
why? 부자인 배우 중에 평론가로부터 나쁜 평을 듣는 배우가 있을 수 있음
ex) Argument : Mark Twain lived in Hannibal, Missouri. Since Sam Clemens was born there, and Mark Twain is Sam Clemens.
– 전제1: Sam Clemens was born in Hannibal, Missouri.
– 전제2: Mark Twain is Sam Clemens.
– 결론: Mark Twain lived in Hannibal, Missouri.
▪ Logically Valid? Yes
▪ Logically Sound? No
– Samuel Clemens (필명 Mark Twain) 은 미주리의 플로리다라는 마을에서 태어남.
-> soundness는 실제로 이 argument가 사실인지를 확인해야 함.
-> 전제에 never, must, all이 있어도 soundness를 확인할 때는 다 믿으면 안 됨.
Arguments 표기법
Fitch Format
- 세로 선으로 argument를 표기
- 가로 선을 이용하여 전제와 결론을 구분
- 가로선 위 : 전제 / 가로선 아래 : 결론
Argument : All rich actors are good actors. Brad Pitt is a rich actor. So, he must be a good actor.

Proof (증명)
: 모든 전제에 해당하는 문장이 참일 때, 결론이 참이라는 것을 한 단계씩 보여주는 것
=> 전제가 주어졌을 때, argument의 logical consequence를 보여주는 것
Informal Proof vs. Formal Proof
Informal Proof

Formal Proof
- Fitch format으로 argument를 나타냄
- 증명 단계를 Fitch bar를 추가해가며 나타냄
- 증명의 정당성 (justification)은 formal system의 규칙을 이용함
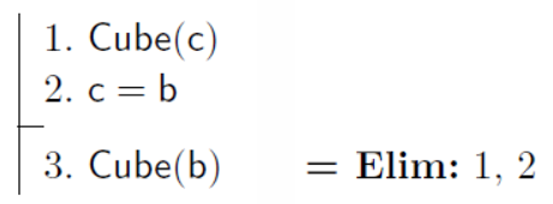
※ 순서
영어로 된 argument를 FOL로 바꾸고 -> Fitch Formet으로 쓴다 -> 증명
validity - 전제가 참이라는 가정 하에
sound - validity를 먼저 보고 전제를 따졌을 때 전제가 모두 참인 경우
Substitution (치환)
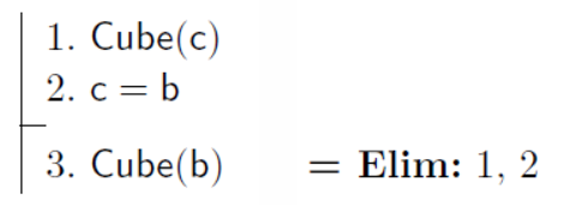
c=b 라는 전제가 있기 때문에, c를 b로 치환하여 결론이 logical consequence
c=b라는 사실이 주어지면, c가 true일 경우에 b도 true가 됨
=> Substitution
철학에서는 indiscernibility of identicals (동일함을 식별) 라고 함
Identity Elimination (=Elim)
: Substitution (치환)을 이용한 증명 원리
= Elim : b=c라면, b가 뭐가 되었든 간에 c로 치환 가능 (indiscernibility of identicals)

※ 치환을 사용한 증명
- 어떤 개체 n이 포함된 문장 P(n)이 참이라는 점을 알고 있고, 문장 n=m이 주어졌을 때,
n을 m으로 치환하여 증명 정당성을 부여
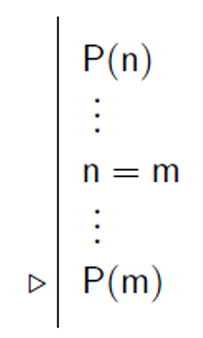
- P(n)과 n=m 두 문장의 순서는 상관이 없음, P(m)만 위 두 문장 후에 나타나면 됨
Identity Introduction (=Intro)
= Intro : FOL에서 b=b라는 문장은 항상 참 (reflexivity of identity)
-> 동일하다는 성질을 반영하여 나타낸 것
전제가 무엇이건 (또는 전제가 없어도) a=a라는 문장은 유효함
why? FOL에서 individual constant로 이름 붙인 개체는 단 하나, 유일하다는 가정을 하고 있기 때문
Identity introduction 을 formal proof 에 적용
Term n 에 대해서 n=n 을 채용(introduction) 가능
어떤 전제가 필요 없고, 이전 단계를 참조(cite)할 필요가 없음
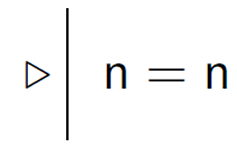
Symmetry of Identity
Argument : From a=b, it is valid that b=a
a=b 라는 전제가 주어졌을 때, b=a라는 결론을 앞서 배운 identity 원리를 이용하여 증명
Informal Proof
- Suppose that a=b. We know that a=a, by the reflexivity of identity. Now substitute the name b for the first use of the name a in a=a, using the indiscernibility of identicals. We come up with b=a, as desired.
-> Informal proof에 정형화 된 증명 규칙은 없지만, 보통 전제를 첫 문장으로 시작하여 단계별 증명 문장을 써서 증명
Transitivity of Identity
: Identity가 옮아가는 성질
ex) a=b와 b=c가 모두 참이라면, a=c 또한 참이 됨
Substitution (or Indiscernibility of identicals)을 써서 증명 가능
Informal proof : 첫째 전제의 b를 c로 치환하여 결론이 참이라는 점을 증명할 수 있음
=> Symmetry of Identity : b=c라면, c=b이다
=> Transitivity of Identity : a=b이고 b=c라면, a=c이다
Formal Proof
- Fitch format으로 증명하는 방법
- 전제 P, Q 그리고 R이 주어졌을 때, 결론 S를 fitch format으로 증명
※ 단계별로 증명 정당성을 명시 해주어야 함

ex) a=b이면, b=a이다
1. 전제와 결론을 나누어 쓰기
-전제 : a=b
-결론 : b=a
2. Fitch Format으로 쓰기
-step by step으로 Fitch bar를 추가
-증명 정당화를 위해 규칙과 참조 번호를 표기

Reiteration (Reit)
- 증명에 반드시 필요한 규칙은 아니지만 증명을 보기에 편하게 만들어줌
- 증명에서 이전 단계를 다시 반복하여 보여줌
- 정당성을 부여할 때는 "Reit: x"로 씀 (x : 라인 번호)
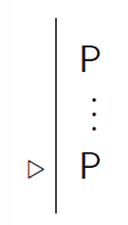
Formal Proof 진행 과정 예시
전제1 : SameRow(a,a)
전제2 : b=a
결론 : SameRow(b,a)는 True
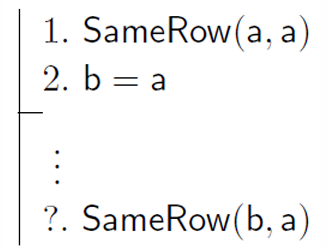


'학교 수업 > 1학년 1학기' 카테고리의 다른 글
| [컴퓨터개론] 컴퓨터의 역사와 구성 (0) | 2024.11.20 |
|---|---|
| [논리학] 6. Formal Proofs and Boolean Logic (0) | 2024.11.18 |
| [논리학] 4. The Logic of Boolean Connectives (4) | 2024.11.18 |
| [논리학] 3. The Boolean Connectives (2) | 2024.11.18 |
| [논리학] 1. Atomic Sentences (0) | 2024.11.18 |



