| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- terms
- identity introduction
- first order logic
- soundness
- individual constants
- disjunction
- Validity
- truth table
- 개별 상수
- conjunction
- 원자 명제
- substitution
- atomic sentence
- formal proof
- functional symbol
- negation
- Connectives
- 논리학
- transitivity of identity
- identity elimination
- reiteration
- predicate symbols
- arguments
- 1차 논리
- fol
- Today
- Total
컴공생의 공부LOG
[논리학] 6. Formal Proofs and Boolean Logic 본문
Introduction Rules & Elimination Rules
Introduction Rules
- 기호를 포함하여 어떤 명제를 증명
ex) a=a (identity introduction)
Elimination Rules
- 특정 기호로부터 어떤 명제를 증명
ex) 1. a=b
2. b=b
3. b=a (identity elimination 2,1)
※ Fitch에서도 적용 가능
Conjunction Rules
- Conjunction ∧ 기호에 관한 증명 규칙
Conjunction Introduction


ex) A∧B∧C 가 주어졌을때, C∧B 를 증명

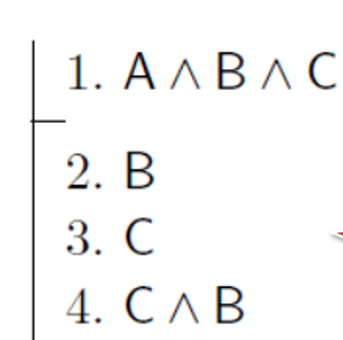


Conjunction Elimation


Disjunction Rules
Disjunction Introduction


Disjunction Elimation
-proof by cases로 부를 수 있음

※ Fitch style에서는 subproof라는 것을 이용
Subproof
- Large proof 안에 끼워서 사용
- Subproof는 보통 가정(assumption)으로 시작
- Fitch bar를 이용하여 subproof를 구분
- Subproof 상의 가정은 오로지 subproof 내에서만 임시로 참이라고 가정하는 것임
- Subproof 이후에 그 안에서 가정 했던 것은 효력이 떨어짐


ex) ( B∧A) ∨(A∧C) 로부터 A를 증명
Disjunction 쪼개기 전 문장과 subproof 들 모두 citation
Subproof 를 cite할 때는 n-m 형태로 줄 번호를 표기

Reiteration 을 이용하는 예시
둘째subproof 에서 가정한 A가 증명하고자 하는목표그 자체라서Reit 을 사용

Negation Rules
Negation Introduction
- proof by contradiction (또는 indirect proof)
- v Elim과 유사하게 subproof가 쓰임
- 어떤 가정 P로부터 모순 ⊥을 이끌어 낼 수 있다면, 본래 전제로부터 ¬P라고 말 할 수 있음

Negation Elimination
- ¬¬P 문장으로부터 P라고 할 수 있음

Contradiction Introduction
- 어떤 문장 P와 ¬P가 성립할 때, 모순⊥이라고함
- (즉, ⊥ Intro)
- 보통 subproof 의 가정이 틀린 것을 보이기위해서, subproof 안에서 사용 (앞장의 subproof 내부에서 일어나는일)

Contradiction Elimination
- Subproof 내에서 가정에 모순 된다는 점을밝혀냈다면, 그 다음 문장은 어떤 문장 P 든지 주장할 수 있음
- 보통 ∨Elim과 함께 사용

왜 ⊥ Elimination이 필요할까?
-> ⊥ Elim 은 증명을 짧게 만들어 주기 때문에 사용
증명 전략
- Argument 자체가 valid 한 지 먼저 생각
- 증명해야 할 결론을 informal하게 먼저 생각해보기
- 결론에서부터 (뒤에서부터) 반대로 거슬러 올라가보기 (결론 바로 앞에 무엇이 있어야 결론이 나올 수 있을지 생각)
'학교 수업 > 1학년 1학기' 카테고리의 다른 글
| [컴퓨터개론] 컴퓨터와 인간의 표현법 (0) | 2024.11.20 |
|---|---|
| [컴퓨터개론] 컴퓨터의 역사와 구성 (0) | 2024.11.20 |
| [논리학] 4. The Logic of Boolean Connectives (4) | 2024.11.18 |
| [논리학] 3. The Boolean Connectives (2) | 2024.11.18 |
| [논리학] 2. The Logic of Atomic Sentences (0) | 2024.11.18 |




