| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- predicate symbols
- transitivity of identity
- atomic sentence
- individual constants
- identity introduction
- truth table
- formal proof
- conjunction
- first order logic
- Validity
- disjunction
- 개별 상수
- Connectives
- fol
- 논리학
- functional symbol
- soundness
- 원자 명제
- terms
- reiteration
- substitution
- negation
- identity elimination
- 1차 논리
- arguments
- Today
- Total
목록2024/11/18 (5)
컴공생의 공부LOG
 [논리학] 6. Formal Proofs and Boolean Logic
[논리학] 6. Formal Proofs and Boolean Logic
Introduction Rules & Elimination RulesIntroduction Rules- 기호를 포함하여 어떤 명제를 증명ex) a=a (identity introduction) Elimination Rules- 특정 기호로부터 어떤 명제를 증명ex) 1. a=b 2. b=b 3. b=a (identity elimination 2,1) ※ Fitch에서도 적용 가능 Conjunction Rules- Conjunction ∧ 기호에 관한 증명 규칙 Conjunction Introduction ex) A∧B∧C 가 주어졌을때, C∧B 를 증명 Conjunction Elimation Disjunction RulesDisjunction Introduction Disjunctio..
 [논리학] 4. The Logic of Boolean Connectives
[논리학] 4. The Logic of Boolean Connectives
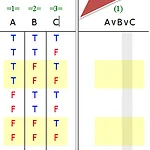
Logical TruthLogical Consequence- 어떤 전제 𝑃1,⋯,𝑃𝑛 로 이루어진 집합에 대하여, 전제들이 모두 참이라고 할 때, 결론 𝑆가 반드시 참인 경우 Logical Truth- 어떤 경우는 전제에 상관없이 또는 전제 자체가 없어도 참인 결론이 있을 수 있음- 필연적으로 참인 문장 예시 : a=a Logical Possibility & Logical NecessityLogical Possibility- 어떤 논리적 상황을 바탕으로 했을 때, 참이 될 수도 있는 경우 Logically possible 예시 문장ex) It is not physically possible to go faster than the speed of light. Logically possible 이 아..
 [논리학] 3. The Boolean Connectives
[논리학] 3. The Boolean Connectives
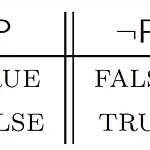
Boolean Connectives (=Truth Functional Connectives)Simple Connectives- Conjunction(= and)- Disjunction(= or)- Negation(= not) -> Truth table을 이용해 complex sentence의 truth 판단을 할 때, complex sentence를 simpler sentence로 쪼갤 때 사용 Negation (¬)- 부정하려는 문장 앞에 붙여 씀 (= not에 대응)- 문장 앞에 몇 개든지 붙여 쓸 수 있음 ex) John isn't home.-> ¬Home(john) ex) 동일성 부정에 사용 가능-> ¬(b=c) -> b ≠ c - Atomic sentence 또는 atomic sent..
 [논리학] 2. The Logic of Atomic Sentences
[논리학] 2. The Logic of Atomic Sentences
Arguments (논의, 논쟁)- 한 개 이상의 전제(premises)와 결론(conclusion)이 모인 일련의 문장 모음※ Functional symbols과 predicate의 인자로 들어가는 인자(argument)와 다른 의미라는 점 주의 ex) All men are mortal. Socrates is a man. So, Socrates is mortal.전제1 : All men are mortal.전제2 : Socrates is a man.결론 : Socrates is mortal. Logically Valid Arguments- Argument 가 주어졌을 때, 아래의 경우 논리적으로 합당(logically valid)한 arguments 라고 함=> 전제가 참일 때, 결론이 참인 경우 Lo..
논리학에서 사용하는 단어 개념 정리Logic (논리)-참/거짓을 가리기 위해 엄격한 검증 원리에 따라서 추론하는 것Syntax (문법)-논리적 문장 구조를 정의하기 위한 논리적 시스템-논리적 문장 구조 정의를 위한 문법※ syntanx에 맞추어 작성해야 syntax error가 발생하지 않음 Semantics (참/거짓)-논리적 문장의 참/거짓-어떤 문장의 semantics? 그 문장의 참 or 거짓을 밝히기※영한사전의 "의미"로 번역하는 것은 바르지 않음 First Order Logic (FOL) (1차 논리)-Individual Constants에만 한정 기호를 가할 수 있고, Predicate에는 한정 기호를 가할 수 없는 논리 체계 Individual Constants (개별 상수)-실제 존재하..
